Calculations involving Masses
Foundation Summary
Giant Covalent
CH78: Calculate Relative Formula Mass
The relative formula mass is simply the atomic masses of all the atoms in a compound added together. You can find the atomic mass in the question – or the big number on the Periodic Table.
Example 1: Chloromethane has the chemical formula of CH3Cl. Calculate the relative formula mass. (Ar: C = 12, H = 1, Cl = 35.5)
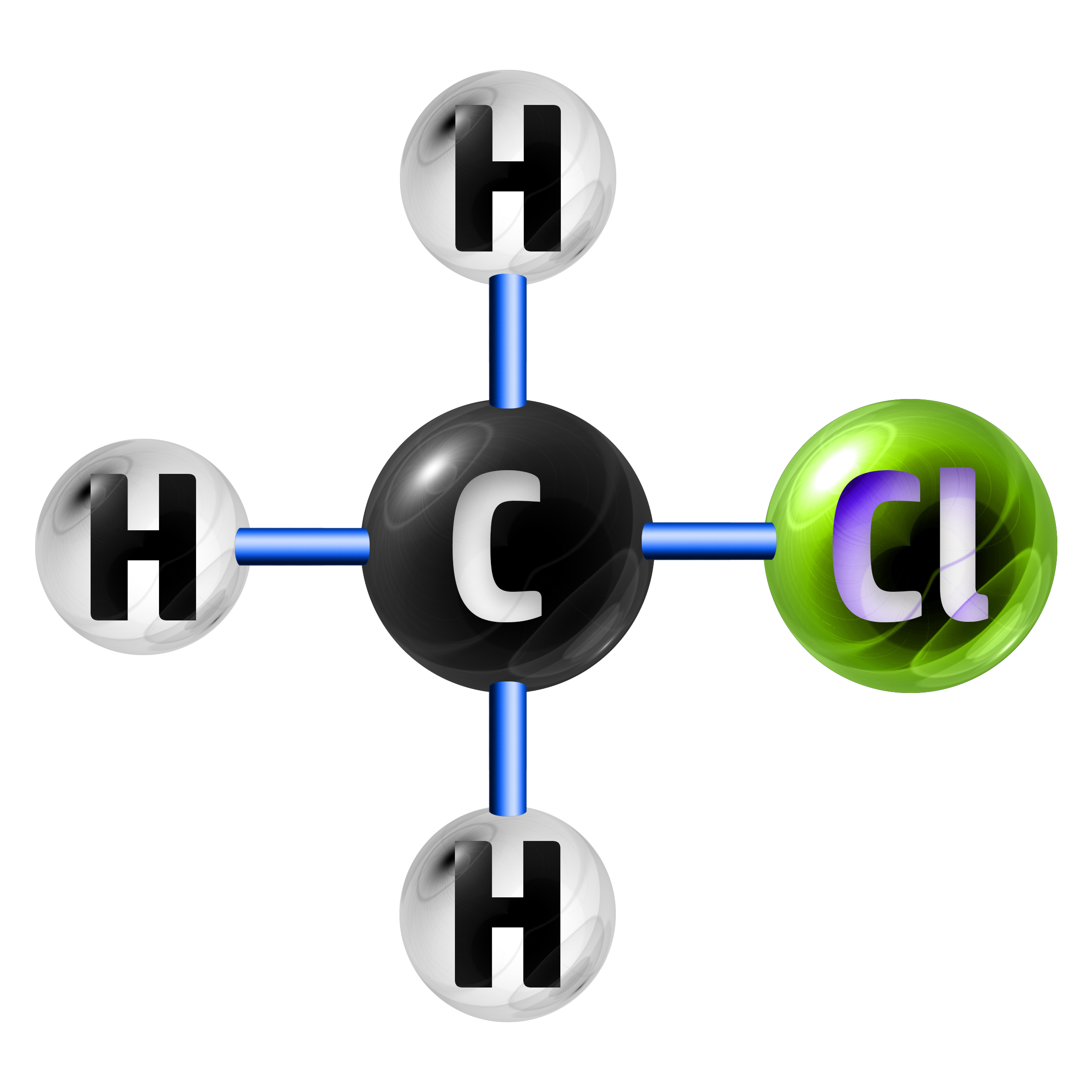
The formula CH3Cl shows me that I have 1 x C (carbon), 3 x H (hydrogen) and 1 x Cl (chlorine).
- 1 x C = 1 x 12 = 12
- 3 x H = 3 x 1 = 3
- 1 x Cl = 1 x 35.5 = 35.5
Relative Formula Mass = 12 + 3 + 35.5 = 50.5
Example 2: Magnesium nitrate has the chemical formula of Mg(NO3)2. Calculate the relative formula mass. (Ar: Mg = 24, N = 14, O = 16)
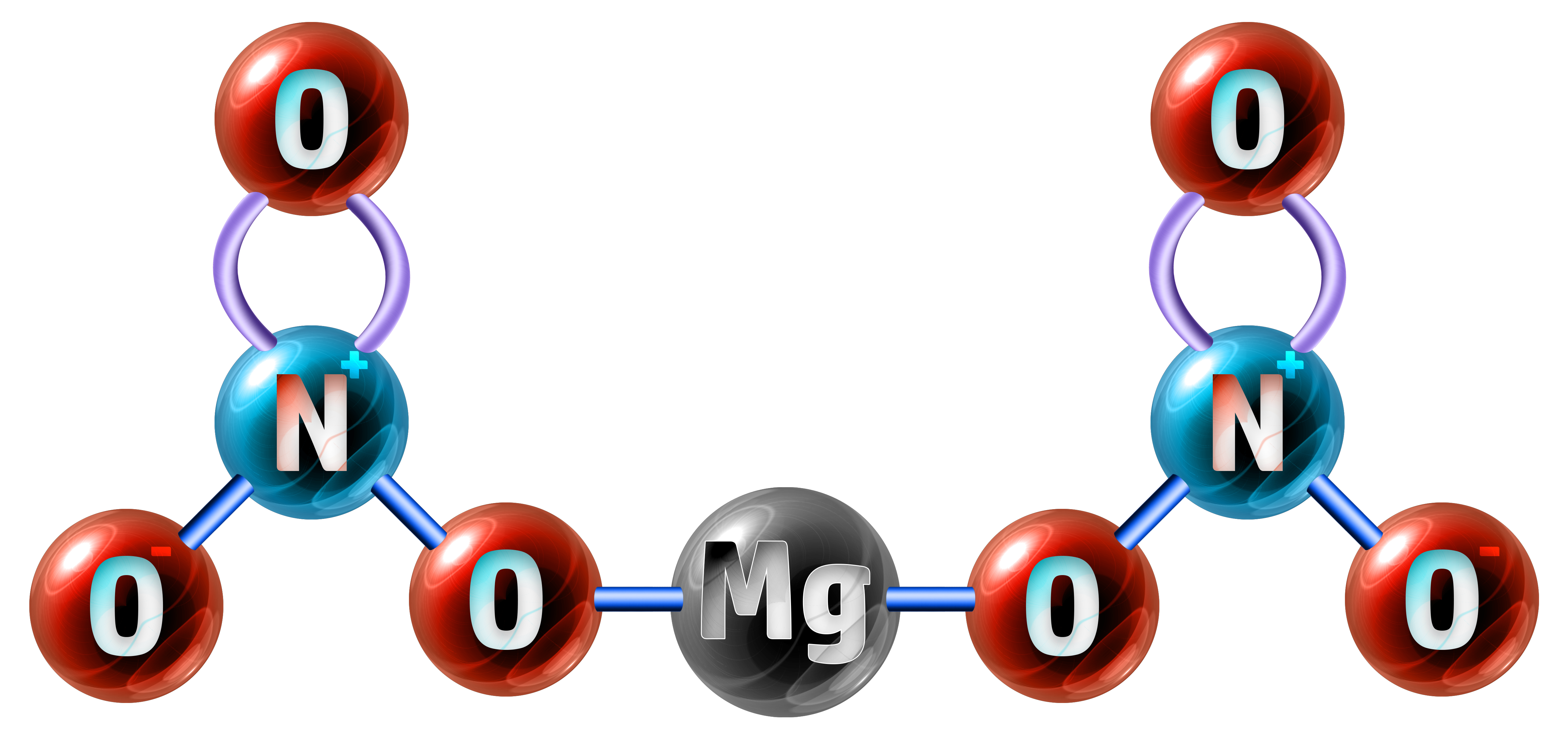
The formula Mg(NO3)2 shows me that I have 1 x Magnesium atom (Mg) connected to two lots of my nitrate ion (NO3), so I have 1x2 nitrogen’s and 3x2 oxygen’s:
- 1 x Mg = 1 x 24 = 24
- 2 x N = 2 x 14 = 28
- 6 x O = 6 x 16 = 96
Relative Formula Mass = 24 + 28 + 96 = 148
CH79: Calculate the empirical formula
Example: 64g of sulfur reacts with 96g of oxygen to produce sulfur oxide. What is the formula of the oxide? (Ar: S = 32, O = 16)
CH80: What is the Empirical formula?
The Empirical formula is the simplest ratio of atoms in a compound:
You can also work backwards.
For example, work out the molecular formula of CH2O when the Mr is 120. (Ar: C = 12, H = 1, O = 1)
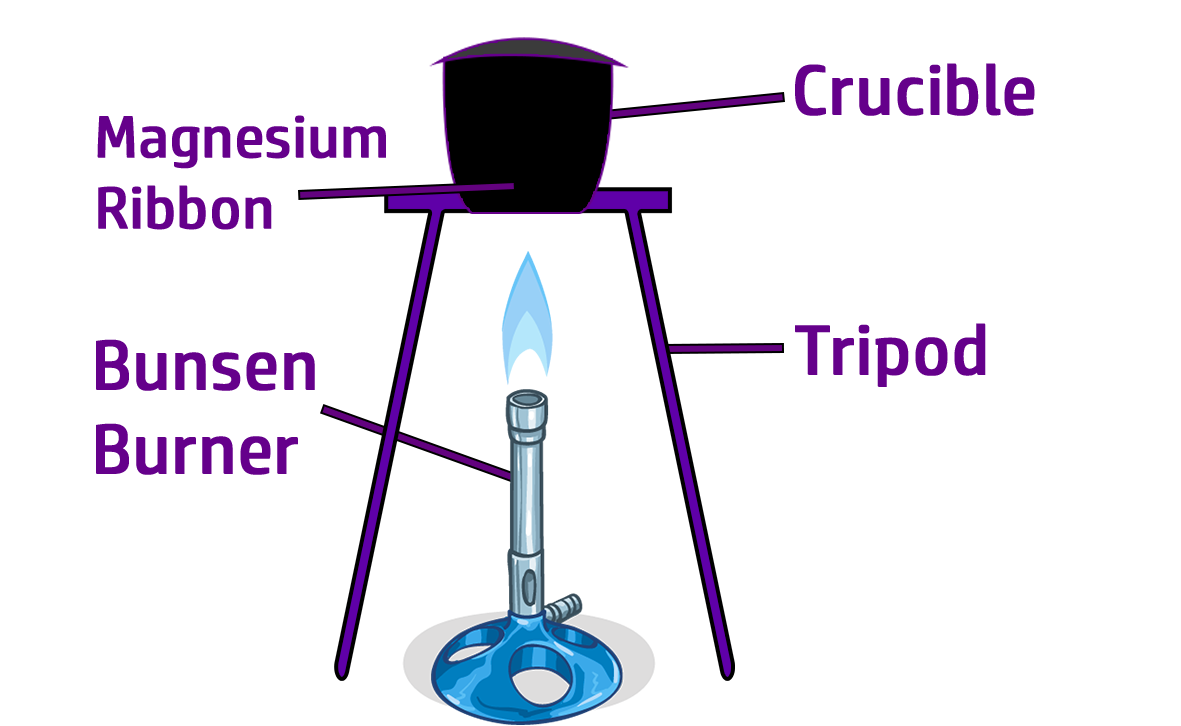
CH81: Investigate the Empirical formula of Magnesium Oxide
If asked to describe a practical to work out the empirical formula of an oxide, do the following:
- Weigh a crucible and lid.
- Weigh a strip of Magnesium.
- Clean the Magnesium strip to remove the oxide layer.
- Heat the magnesium strongly in a crucible, lifting the lid of the crucible to replenish (add more) oxygen.
- Once the magnesium has fully reacted and is a white powder, reweigh the crucible, lid, and magnesium oxide.
- Subtract the mass of the crucible and lid to leave you with the mass of magnesium oxide.
- Calculate the empirical formula (CH79).
CH82: Explain the conservation of mass
The conservation of mass states that the total mass of reactants is always the same as the total mass of products.
So, if you added 5g of sodium to 100g of water you would end up with 105g of sodium hydroxide and hydrogen gas combined.
The mass may appear to go down in the above reaction – and if it does it is because a gas (such as hydrogen) has escaped.
To prove that the mass stays the same use a sealed container. I.e., Add a lid!
CH83: Calculate Maximum Masses
Example: Work out how much sodium chloride is produced when 5.3g of sodium carbonate reacts with excess dilute hydrochloric acid. (Ar: Na = 23, C = 12, O = 16, H = 1, Cl = 35.5).
There are two ways you can answer this question:
Both methods give the same answer – so go with what you feel more confident with!
CH84: Calculate concentration in gdm-3
To calculate the concentration of a solution in grams per decimetre cubed (gdm-3), you need two things: the mass in grams, and the volume in dm3 (cm3 / 1000)
Example: 20g of sodium hydroxide dissolves in 750cm3 of water. Calculate the concentration in gdm-3
- Volume = 750cm3 / 1000 = 0.75dm3
- Concentration = mass / volume = 20g / 0.75dm3 = = 26.7gdm-3
CH85: Moles and Avogadro's Constant (H)
Every time you see a balanced equation you are seeing a ratio – how much of each substance is needed:
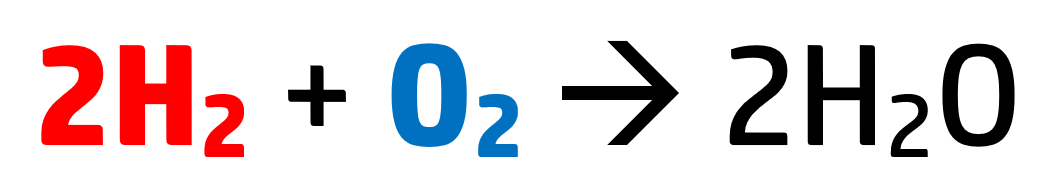
This reaction shows that for every molecule of oxygen, you need two molecules of hydrogen.
These numbers represent moles, and a mole represents 6.02x1023 {atoms / molecules / particles} of that substance.
For example, in the above reaction, we have 2 moles of hydrogen – meaning we have 2 x 6.02x1023 molecules of hydrogen (which is 1.204x1024 particles of hydrogen).
Oxygen just has 1 mole, so has 6.02x1023 particles. This number – 6.02x1023 – is known as Avogadro’s constant.
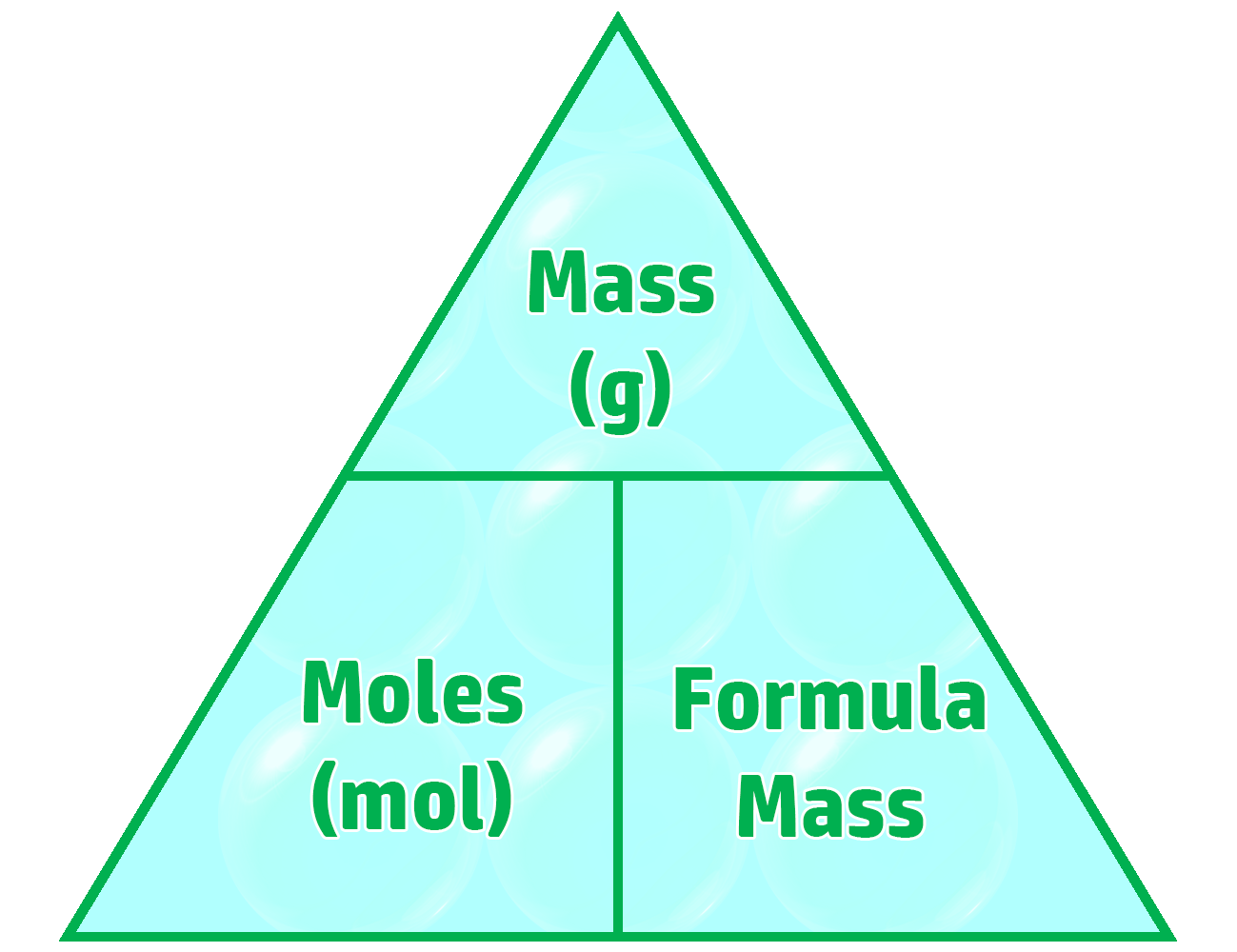
CH86: Calculate moles, mass and formula mass (H)
Moles (along with Avogadro’s constant – CH85) represent how many particles of a substance you have.
This can be calculated by using the triangle on the right.
For example: How many moles of sodium chloride, NaCl, are there in 5g of the compound? (Ar: Na = 23, Cl = 35.5)
- Step 1: Work out the formula Mass (CH78) = 23 + 35.5 = 58.5
- Step 2: Divide the mass (g) by the formula mass = 5g / 58.5 = 0.085 mol
You can also work out the exact number of particles of each substance.
In the above example, we have worked out that we have 0.085 moles of sodium chloride.
To work out the particles, just multiply this number by Avogadro’s constant – which they will always give you in the question (6.02x1023) = 0.085 x 6.02x1023 = 5.12x1022 particles of sodium chloride.
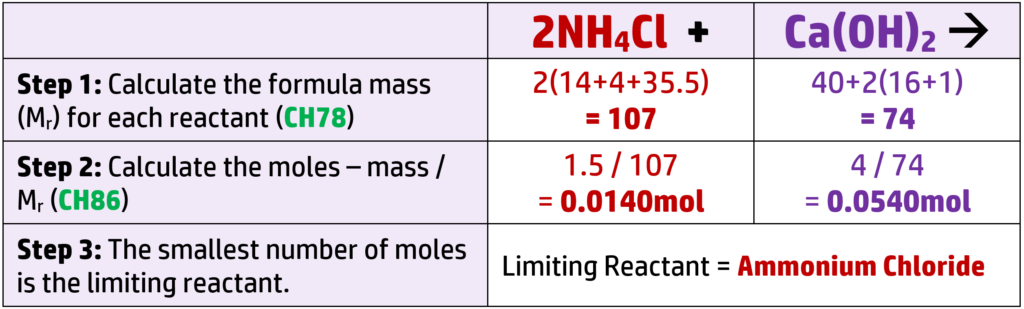
CH87: Calculate the limiting reactant for a reaction (H)
The limiting reactant is the reactant that you will run out of first. Once this runs out, the reaction will stop.
Example: 1.50g of ammonium chloride reacts with 4.0g of calcium hydroxide to form ammonia.
Work out the limiting reactant. (Ar: N = 14, H = 1, Cl = 35.5, Ca = 40, O = 16)
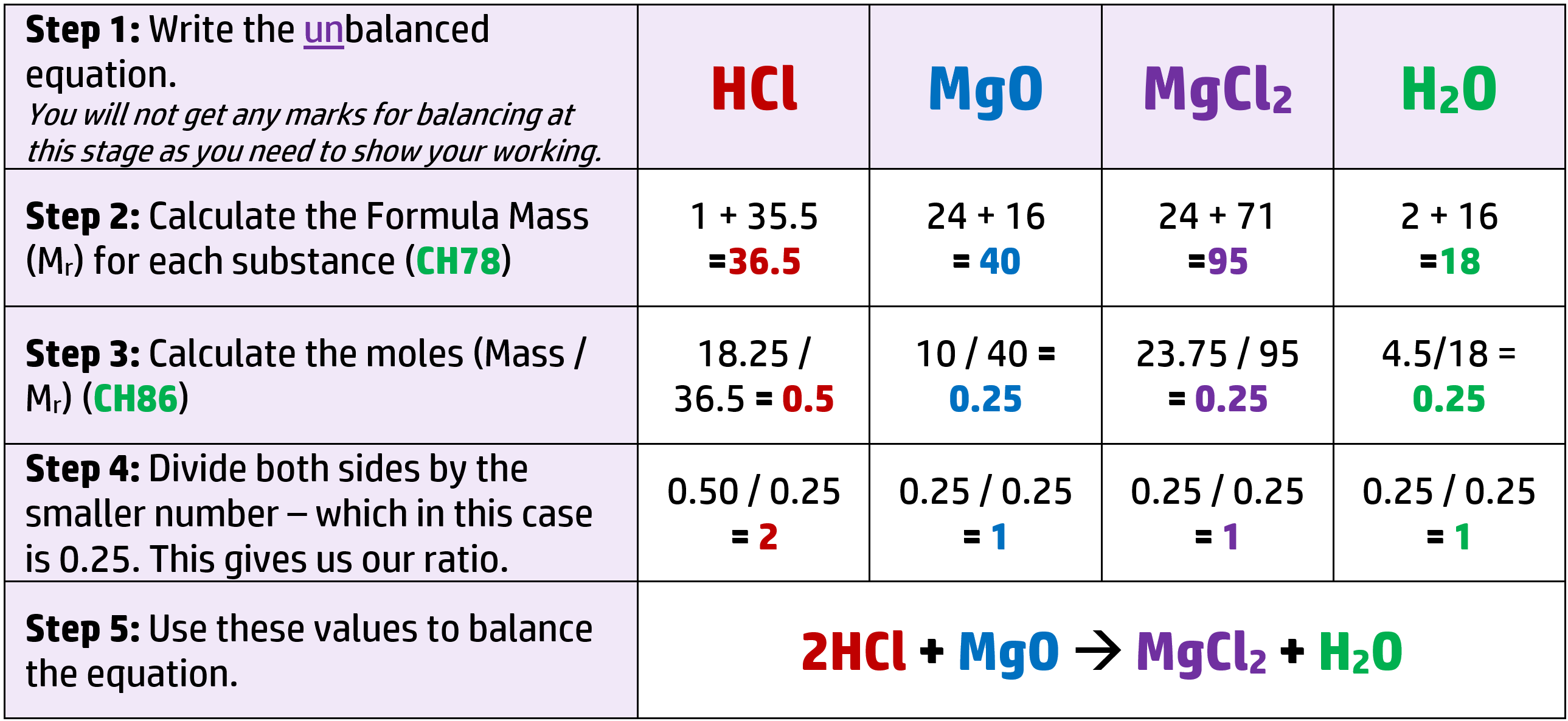
CH88: Balance chemical equations using stoichiometry (H)
You won’t normally see the term “stoichiometry” in the exam, but will see a question similar to the below:
Example 1: 18.25g of hydrochloric acid, HCl, reacts with 10g of Magnesium oxide, MgO, to form 23.75g of magnesium chloride, MgCl2 and 4.5g of water. Deduce the balanced equation for the reaction.
You must show your working. (Ar: H = 1, Cl = 35.5, Mg = 24, O = 16)
